The "Critical Power" Concept and High-Intensity Exercise Performance

KEY POINTS

• The curvilinear relationship between power output and the time for which it can be sustained is a fundamental feature of high-intensity exercise performance. This relationship levels off at a “critical power” (CP) that separates power outputs that can be sustained in a physiological “steady-state” from those that cannot.
• The curvature of the power-time relationship (the so-called W′), which represents the amount of work that can be done during exercise above CP, is constant and is utilized at different rates depending on the proximity of the exercise power output to CP.
• Traditionally, the CP model has been used to provide insights into physiological responses, fatigue mechanisms and performance during continuous constant power output exercise. However, in recent years, the appeal of the CP concept has been broadened through its application to intermittent high-intensity exercise.
• With the assumptions that W′ is utilized during work intervals above CP and reconstituted during recovery intervals below CP, it can be shown that performance during intermittent exercise is related to four factors: the intensity and duration of the work intervals, and the intensity and duration of the recovery intervals. However, while the utilization of W′ may be assumed to be linear, the reconstitution kinetics of W′ appears to be curvilinear and to be highly variable among individuals.
• This has led to the development of a new CP model for intermittent exercise in which the balance of W′ remaining (W′_BAL) may be calculated. The W′_BAL model may have exciting applications in the real-time monitoring of athlete fatigue progression in endurance and team sports.

INTRODUCTION

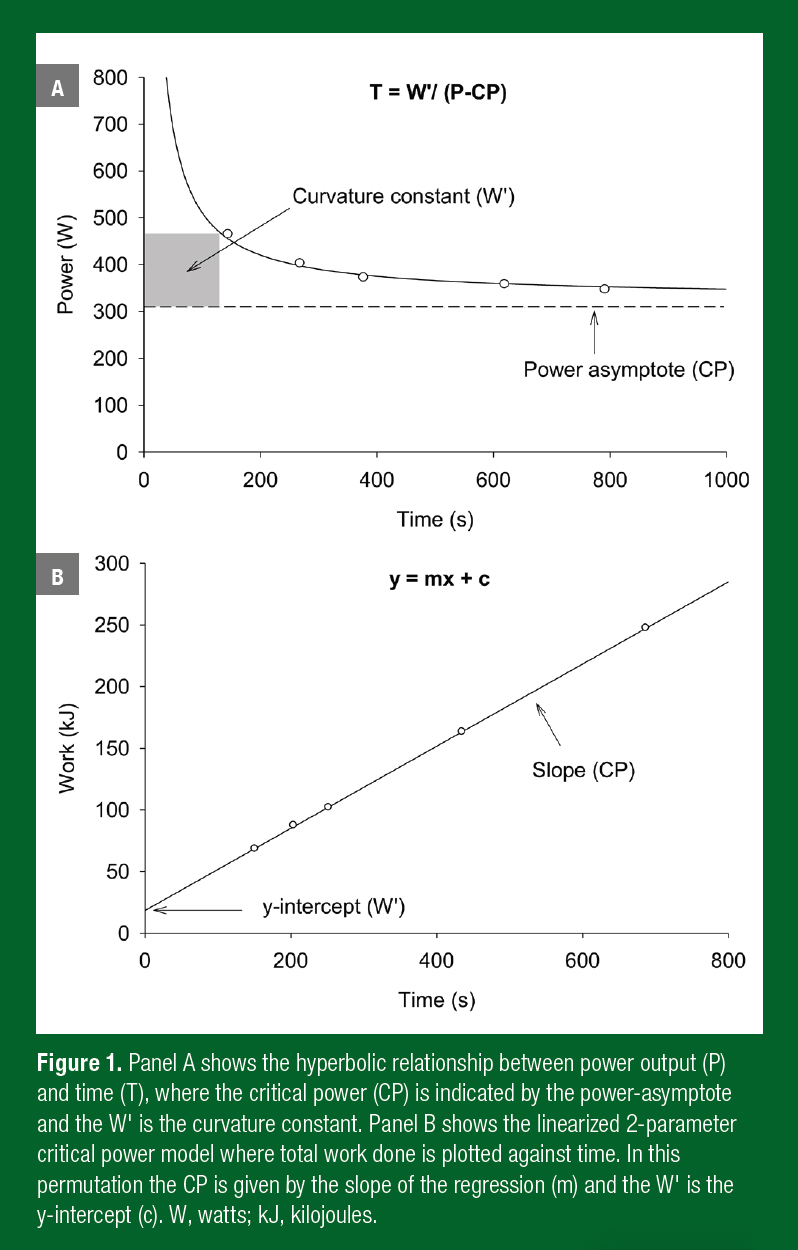
The hyperbolic relationship between power output and the time for which it can be sustained is well established in exercise physiology (Hill, 1925; Monod & Scherrer, 1965; Poole et al., 1988). This relationship is typically established by having a subject complete between 3 and 5 separate high-intensity exercise tests on different days, during which they are asked to sustain a fixed external power output for as long as possible. The power outputs are selected to result in “exhaustion” in a minimum of ~2 min and a maximum of ~15 min. The subject’s precise “time to the limit of tolerance” at each of these power outputs is recorded. When power output is subsequently plotted against time, it can be observed that the sustainable power output falls as a function of the exercise duration and that it will eventually level off or reach an asymptote (Figure 1A). This asymptote has been termed the critical power (CP) which is measured in Watts (W). The curvature of the power-time relationship, which represents the work capacity available above CP, has been termed W′ which is measured in kilojoules (kJ). The information contained in this “curvilinear” power-time relationship can also be expressed if work done in each of the separate exercise bouts is plotted against sustainable time. This results in a more “user-friendly” linear relationship which can be described with the regression equation y = mx + c, where the slope m is CP and the intercept c is W′ (Figure 1B). It is important to note that while the description given above relates to power output, and the majority of the related research has employed cycle ergometry, this same relationship exists in other modes of human locomotion, including running (Hughson et al., 1984) and swimming (Wakayoshi et al., 1992). In these situations, the terms critical speed (CS, or velocity (CV) in m/s) and D’ (m) are used instead of CP and W′.

Physiologically, CP is important because it defines the boundary between discrete domains of exercise intensity (Jones et al., 2008; Poole et al., 1988; Vanhatalo et al., 2016). Below CP, in the “heavy” intensity domain, “steady-state” values for muscle metabolites (for example, phosphocreatine concentration ([PCr]), inorganic phosphate concentration and pH), as well as blood [lactate], and o₂ can be attained. Above CP, in the “severe” intensity domain, however, these variables do not demonstrate steady-state behavior. Rather, despite the external power output remaining constant, muscle efficiency is lost, as reflected in the development of a “slow component” of o₂ (Poole et al., 1988; Vanhatalo et al., 2016). Exercise in the severe domain is also associated with continuous reductions in muscle [PCr] and pH, and a progressive accumulation of blood lactate, until the limit of tolerance is reached. It is interesting that these respective minimum and maximum values are similar irrespective of whether the severe-intensity exercise bout is relatively short (2-3 min) or relatively long (12-15 min) (Vanhatalo et al., 2010). This suggests that the limit of tolerance during such exercise may coincide with the attainment of a certain intramuscular and/or systemic milieu which the subject cannot, or is not prepared to, exceed.

The CP may be functionally defined as the highest power output that can be sustained without progressively drawing on W′, where the latter represents, at the onset of exercise, a fixed amount of work that can be done when CP is exceeded. If the power output being sustained was considerably above CP such that the tolerable duration of exercise was short, W′ would be utilized at a more rapid rate than would be the case if the power output being sustained was only just above CP and exercise duration was correspondingly longer. While it is tempting to consider W′ as an “anaerobic” capacity, comprising energy that may be derived from substrate-level phosphorylation as well as stored O₂, observations of inter-relationships between CP and W′ suggest that this may be an oversimplification (Poole et al., 2016).

It is important to appreciate that performance in the severe-intensity domain (which encompasses a rather large swathe of athletic events, for example, in track and field, from 800 m up to perhaps 10,000 m), depends upon both CP and W′. While CP will reflect the highest sustainable oxidative metabolic rate, the size of W′ will determine the sustainable duration of exercise above that metabolic rate. Knowledge of an athlete’s CP and W′ permits a coach or sports scientist to calculate that athlete’s best possible time for a given distance and to consider tactical and pacing strategies that might optimize performance relative to the athlete’s competitors (Morton, 2009; Vanhatalo et al., 2011).     

While the parameters that may be extracted from the power-time relationship have many valuable applications in sport, a key limitation is that they are conventionally derived entirely on the basis of performance during constant power output exercise. Such a scenario is rather rare in “real world” sport. Many sports, especially team sports, involve intermittent bouts of high-intensity exercise separated by variable durations of lower-intensity exercise or rest, and even “continuous” sports events often involve variations in pacing due to terrain, environmental conditions and the tactics employed by the athlete and his or her competitors. Moreover, if the CP concept is to be extended to the prescription and evaluation of training, then it would be advantageous if this could encompass intermittent as well as continuous exercise because most athletic training programs involve both interval training and steady-state aerobic exercise. The purpose of this Sports Science Exchange article is to provide an overview of emerging applications of the CP concept in sport with particular emphasis on variable-power and intermittent exercise.         

RESEARCH REVIEW

As described above, the power-time parameters are typically derived from several exhaustive exercise bouts completed at discrete but constant power outputs, with W′ so derived being considered as a fixed amount of work that can be done above CP. However, whether W′ is indeed fixed when severe-intensity exercise is performed not at a constant power output but with different pacing strategies has received limited attention. Chidnok et al. (2013a) estimated CP and W′ from a 3-min all-out test (3AOT) and then calculated the work done above CP during different forms of maximal exercise, including a ramp incremental exercise test, a constant power output test where the predicted exercise duration was 3 min, and a test where the subjects were instructed to complete as much work as possible in 3 min and could choose their own pacing strategy to achieve this goal. The total work done above CP was not significantly different between conditions, being close to 16 kJ for 3AOT, incremental exercise constant power output exercise, and self-paced exercise. The maximum o₂ value that was attained was also not different among the four conditions. This indicates that the limit of tolerance during severe-intensity exercise coincides with the achievement of the same o_2­ max and completion of the same amount of work above CP, irrespective of the exercise protocol or pacing strategy employed. This is important as a first step toward applying the CP concept to variable-power exercise, which is common in field-based training and competition.

Physiological responses in recovery from severe-intensity exercise

The CP concept predicts that recovery from exhaustive severe-intensity exercise requires the power output to be reduced below CP. The finite W′ is only utilized above CP, and because CP reflects the highest sustainable oxidative metabolic rate, exercise below CP should theoretically permit some “oxidative metabolic reserve” to be used for recovery processes (e.g., replenishment of high-energy phosphates, H⁺ clearance). This hypothesis was tested by Chidnok et al. (2013c). In this study, subjects completed knee-extension exercise to exhaustion (for ~180 s) on three occasions, followed by a “recovery” period involving: 1) exercise at a lower power output but still within the severe-intensity exercise domain; 2) heavy-intensity exercise; or 3) a 10-min passive recovery period, while the muscle metabolic responses to exercise were assessed using ³¹P magnetic resonance spectroscopy (³¹P-MRS). There was a significant difference between the sustainable exercise duration during the recovery from exhaustive severe-intensity exercise between the <CP and >CP conditions (at least 10 min and ~39 s, respectively). During passive recovery and <CP recovery exercise, muscle [PCr] and pH increased rapidly, approaching baseline values after 10 min. However, when the “recovery” exercise remained >CP, neither muscle [PCr] nor pH recovered, remaining at the nadir reached at the termination of the initial exercise bout. These results confirm that the muscle metabolic dynamics in recovery from exhaustive severe-intensity exercise differ according to whether subsequent exercise is performed below or above CP. This has important implications for the development of a model to explain and predict high-intensity intermittent exercise performance.

Application of the CP concept to intermittent exercise

Morton and Billat (2004) were the first to consider the development of a CP model for intermittent exercise. These authors recognized that intermittent exercise tolerance is a function of four independent variables: work interval power output (P_W), work interval duration (D_W), recovery interval power output (P_R) and recovery interval duration (D_R). For the model to be valid, the power output for the work intervals must be above CP, the power output for the recovery intervals must be below CP, and the mean power output for the session must be above CP (if not, the exercise could theoretically continue indefinitely). Within these restrictions, Morton and Billat (2004) showed that if one of P_W, D_W or P_R is increased while the other variables are held constant, exercise tolerance is reduced; however, if D_R is increased while the other variables are held constant, exercise tolerance is increased.

To test some of the assumptions inherent in the model of Morton and Billat (2004), Chidnok et al. (2012) determined CP and W′ with the 3AOT and then asked subjects to complete a severe-intensity constant power output cycle test (S-CPO) and four further tests to exhaustion using different intermittent protocols (i.e., severe-severe (S-S), severe-heavy (S-H), severe-moderate (S-M) and severe-light (S-L)) to the limit of tolerance. In this set of experiments, P_W was held constant, D_W was held constant at 60 s, and D_R was held constant at 30 s; only P_R was manipulated. The tolerable duration of exercise in S-CPO was ~384 s and, as hypothesised, exercise tolerance was progressively increased when P_R was reduced (i.e., by 47%, 100% and 219%, for S-H, S-M, and S-L, respectively). The greater exercise tolerance at lower P_R was linearly related to the total work done above CP which, compared with S-CPO (~23 kJ), was significantly and progressively greater for S-H, S-M and S-L. Using the known values of CP, P_W and D_W, Chidnok et al. (2012) calculated how much W′ was utilized in each work interval and, assuming that W′ was fully utilized at the limit of tolerance, also calculated the extent of W′ reconstitution during each recovery interval. The results indicated that W′ is reconstituted more rapidly when there is a greater difference between CP and P_R.

Chidnok et al. (2013b) extended their observations by investigating the influence of altering D_R on muscle metabolic responses (measured with ³¹P-MRS) and exercise tolerance during knee extension exercise. In this study, P_W and D_W were held constant, but subjects were asked to exercise to the limit of tolerance on three occasions with passive (i.e., P_R = 0 W) recovery durations of 18 s, 30 s or 48 s. The tolerable duration of exercise was ~304 s, ~516 s, and ~847 s for the 18 s, 30 s and 48 s recovery protocols, respectively. The restoration of muscle [PCr] (as well as [ADP] and [P_i]) during recovery was greatest, intermediate, and least for 48 s, 30 s, and 18 s of recovery, respectively. Consistent with Chidnok et al. (2012), the total work done above CP was significantly greater for all intermittent protocols compared with the subjects' W′. This difference became progressively greater as D_R was increased and was significantly correlated with the mean magnitude of muscle [PCr] reconstitution between work intervals. These results indicate that during intermittent high-intensity exercise, recovery intervals allow the concentrations of high-energy phosphates to be partially restored, with the degree of restoration being related to the duration of the recovery interval. Consequently, the ability to perform work above CP during intermittent high-intensity exercise and, therefore, exercise tolerance, increases when recovery-interval power output is lower (Chidnok et al., 2012) or longer in duration (Chidnok et al., 2013b).

One assumption made in the above studies was that W′ reconstitution in recovery is a linear process with a fixed rate (in J·s^-1) for the duration of each recovery period. To examine this, Ferguson et al. (2010) examined the time course of W′ reconstitution by asking subjects to complete a series of conventional constant power output exercise bouts at discrete time points (2, 6 and 15 min) following an initial bout of exhaustive severe-intensity exercise. In each case, the hyperbolicity of the power-time relationship was preserved and CP was not significantly different from that measured in the control (unfatigued) condition. In contrast, W′ was significantly different in each condition, being approximately 22 kJ in the control condition and 8 kJ, 14 kJ and 19 kJ when measured after 2, 6 and 15 min recovery from exhaustive exercise, respectively. From the 3 time points studied (2, 6 and 15 min), Ferguson et al. (2010) observed that W′ was reconstituted more rapidly in the early compared to the late recovery period, i.e., the pattern of W′ reconstitution appeared to be curvilinear rather than linear.

Building on this, Skiba et al. (2012) applied a continuous equation to model W′ reconstitution kinetics during intermittent exercise (the W'_BAL model). The relationship was best fit with an exponential with the time constant for W′ reconstitution being negatively related to the difference between CP and the recovery power output, i.e., W′ was reconstituted more rapidly when P_R was smaller. The time constant for W′ reconstitution was ~377 s when recovery occurred at 20 W, ~ 452 s when recovery occurred in the moderate-intensity domain and ~580 s when recovery occurred in the heavy-intensity domain. The W′ reconstitution time constant increased to non-physiological values when the P_R remained above CP, indicating no net recharge of W′ but merely a slower rate of W′ utilization in the recovery intervals compared to the work intervals.

Having described the relationship between recovery power output and the kinetics of W′ reconstitution, Skiba et al. (2014b) next evaluated the effects of work and recovery interval duration on W′ kinetics. Subjects completed severe-intensity intermittent exercise, using six different combinations of work and recovery interval durations, until they had utilized 50% of their predicted W′_BAL. Following each of the intermittent exercise protocols, subjects exercised at a constant severe-intensity power output until the limit of tolerance. The actual W′ measured during the constant power output test was then compared with the amount of W′ predicted to be available by the W'_BAL model. Differences between actual W′ and W′_BAL were generally small, amounting to only ~1.6 kJ when averaged across conditions (i.e., within ~10% of W′). That W′_ACT was, for the most part, accurately predicted in this study indicates that variations in work and recovery durations during intermittent exercise did not adversely influence model outcomes, therefore supporting the validity of the W′_BAL model.

PRACTICAL APPLICATIONS

The validity of the W′_BAL model in the field was tested by Skiba et al. (2014a). Data were collected from the bicycle power meters of eight trained triathletes. For all files, W′_BAL was calculated and then compared between situations where the athletes reported becoming prematurely exhausted during training or competition and situations where the athletes successfully completed a difficult assigned task or race. Calculated W′_BAL was significantly different between the two situations: in the first situation, the mean W′_BAL at exhaustion was just 0.5 ± 1.3 kJ, whereas the minimum W′_BAL in the non-exhausted situation was 3.6 ± 2.0 kJ. Receiver-operator-characteristic curve analysis indicated that the W′_BAL model is useful for identifying the point at which athletes are in danger of becoming exhausted.

Although further refinement may be required, the W′_BAL model appears to represent an important new development in assessing athlete fatigue state and current performance capacity during training and racing. The apparent ability of the model to track the dynamic state of W′ during intermittent exercise may have important implications for the planning and real-time monitoring of athletic performance. From a bioenergetic perspective, avoiding frequent or protracted excursions beyond CP, except perhaps when tactically necessary or in a sprint finish, would seem sensible to prevent premature or excessive utilization of W′ and the associated muscle metabolic and systemic perturbations which would expedite fatigue. A wristwatch or handlebar-mounted monitor programmed to provide an endurance athlete with real-time feedback on the percentage of W′ remaining during competition could therefore provide critical information on optimal pacing strategy (i.e., whether or not to initiate a break or to respond to an attempted break by a competitor).

In the future, it might also be possible for coaches to remotely monitor W′ remaining in players engaged in team sports and to use the data to inform decisions on rotations or substitutions. Another application of the W′_BAL model is in the development of individualised interval training sessions. With knowledge of an athlete’s CP, W′ and W′ recovery kinetics, a coach may be able to prescribe work and recovery interval intensities and durations with greater precision to achieve specific physiological goals.

SUMMARY

In conclusion, the hyperbolic power-time relationship provides an essential foundation for understanding the physiological bases to fatigue development in different exercise intensity domains. For continuous exercise, the CP model has found many important uses in performance modeling and training prescription. Recently, increasing attention has focused on applying the CP model to intermittent exercise. Performance during such exercise depends essentially on the individual’s CP and W′, the work interval power output and duration, and the recovery interval power output and duration. However, whereas W′ may be utilized linearly when power output exceeds CP, W′ may not necessarily be reconstituted linearly, a factor that is accounted for in the W′_BAL model. A large number of popular team sports (e.g., football, rugby, hockey, basketball) are characterized by frequent bursts of severe-intensity exercise interspersed by lower-intensity recovery periods. Application of the CP model may enable a better understanding of the limitations to performance in such sports and therefore inform competition tactics and training practices.

REFERENCES

Chidnok, W., F.J. Dimenna, S.J. Bailey, A. Vanhatalo, R.H. Morton, D.P. Wilkerson, and A.M. Jones (2012). Exercise tolerance in intermittent cycling: application of the critical power concept. Med. Sci. Sports Exerc. 44:966-976.

Chidnok, W., F.J. Dimenna, S.J. Bailey, D.P. Wilkerson, A. Vanhatalo, and A.M. Jones (2013a). Effects of pacing strategy on work done above critical power during high-intensity exercise. Med. Sci. Sports Exerc. 45:1377-1385.

Chidnok, W., F.J. Dimenna, J. Fulford, S.J. Bailey, P.F. Skiba, A. Vanhatalo, and A.M. Jones (2013b). Muscle metabolic responses during high-intensity intermittent exercise measured by ³¹P-MRS: relationship to the critical power concept. Am. J. Physiol. 305:R1085-R1092.

Chidnok, W., J. Fulford, S.J. Bailey, F.J. Dimenna, P.F. Skiba, A. Vanhatalo, and A.M. Jones (2013c). Muscle metabolic determinants of exercise tolerance following exhaustion: relationship to the "critical power". J. Appl. Physiol. 115:243-250.

Ferguson, C., H.B. Rossiter, B.J. Whipp, A.J. Cathcart, S.R. Murgatroyd, and S.A. Ward (2010). Effects of recovery duration from prior exhaustive exercise on the parameters of the power-duration relationship. J. Appl. Physiol. 108:866-874.

Hill, A.V. (1925). The physiological basis of athletic records. Nature 116:544-548.

Hughson, R.L., C.J. Orok, and L.E. Staudt (1984). A high velocity treadmill running test to assess endurance running potential. Int. J. Sports Med. 5:23-25.

Jones, A.M., D.P. Wilkerson, F. DiMenna, J. Fulford, and D.C. Poole (2008). Muscle metabolic responses to exercise above and below the “critical power” assessed using ³¹P-MRS. Am. J. Physiol. 294:R585-R593.

Monod, H., and J. Scherrer (1965). The work capacity of a synergic muscular group. Ergonomics 8:329-338.

Morton, R.H. (2009). Isoperformance curves: an application in team selection. J. Sports Sci. 27:1601-1605.

Morton, R.H., and L.V. Billat (2004). The critical power model for intermittent exercise. Eur. J. Appl. Physiol. 91:303-307.

Poole, D.C., M. Burnley, A. Vanhatalo, H.B. Rossiter, and A.M. Jones (2016). Critical power: an important fatigue threshold in exercise physiology. Med. Sci. Sports Exerc. 48:2320-2334.

Poole, D.C., S.A. Ward, G.W. Gardner, and B.J. Whipp (1988). Metabolic and respiratory profile of the upper limit for prolonged exercise in man. Ergonomics 31:1265-1279.

Skiba, P.F., W. Chidnok, A. Vanhatalo, and A.M. Jones (2012). Modeling the expenditure and reconstitution of work capacity above critical power. Med. Sci. Sports Exerc. 44:1526-1532.

Skiba, P.F., D. Clarke, A. Vanhatalo, and A.M. Jones (2014a). Validation of a novel intermittent W′ model for cycling using field data. Int. J. Sports Physiol. Perform. 9:900-904.

Skiba, P.F., S. Jackman, D. Clarke, A. Vanhatalo, and A.M. Jones (2014b). Effect of work and recovery durations on W′ reconstitution during intermittent exercise. Med. Sci. Sports Exerc.46:1433-1440.

Vanhatalo, A., M.I. Black, F.J. DiMenna, J.R. Blackwell, J.F. Schmidt, C. Thompson, L.J. Wylie, M. Mohr, J. Bangsbo, P. Krustrup, and A.M. Jones (2016). The mechanistic bases of the power-time relationship: muscle metabolic responses and relationships to muscle fibre type. J. Physiol. 594:4407-4423.

Vanhatalo, A., J. Fulford, F.J. DiMenna, and A.M. Jones (2010). Influence of hyperoxia on muscle metabolic responses and the power-duration relationship during severe-intensity exercise in humans: a ³¹P magnetic resonance spectroscopy study. Exp. Physiol. 95:528-540.

Vanhatalo, A., A.M. Jones, and M. Burnley (2011). Application of critical power in sport. Int. J. Sports Physiol. Perform. 6:128-136.

Wakayoshi, K., K. Ikuta, T. Yoshida, M. Udo, T. Moritani, Y. Mutoh, and M. Miyashita (1992). Determination and validity of critical velocity as an index of swimming performance in the competitive swimmer. Eur. J. Appl. Physiol. Occup. Physiol. 64:153-157.