Sodium Ingestion, Thirst and Drinking During Endurance Exercise
KEY POINTS
- Most medical scientific organizations recommend low or moderate sodium diets to the general population in order to reduce the risk of high blood pressure (hypertension).
- Regular physical activity reduces the risk of hypertension.
- Athletes lose sodium in sweat during exercise. The amount of sodium that is lost during endurance exercise depends on the sweating rate and the concentration of sodium in the sweat. In turn, sodium loss during exercise depends on individual factors, such as genetics, fitness and heat acclimatization, as well as the type, intensity and duration of exercise and the external environment.
- Sodium ingestion by endurance athletes does not typically increase blood pressure, so low sodium diets are not recommended for individuals who participate in long-term aerobic exercise.
- Sodium ingestion during or following endurance exercise will help to stimulate thirst and drinking as well as stimulate fluid retention by the kidney.
- No athletes are immune to hypertension, so athletes should monitor their blood pressure as they do their general health. This is particularly important for older athletes, athletes with a genetic predisposition to hypertension, stroke or other cardiovascular disease.
INTRODUCTION
Sodium is an essential electrolyte for cell function, body fluid and blood pressure regulation, blood volume and pH. However, excess sodium can promote hypertension in some individuals, the effects of which are a leading cause of death in the U.S. The average American diet provides approximately three times the recommended level of sodium intake.
The American Heart Association recommends reducing sodium from the diet and suggests a sodium intake of 1,500 mg/d on its website. The most respected U.S. scientific bodies, including the National Institutes of Health and the Institute of Medicine, also recommend that most Americans reduce sodium intake in their diets to reduce strain on the kidney and cardiovascular system, and reduce the risk of hypertension. Indeed, excessive or chronically high sodium in the diet can increase the risk of hypertension in some groups of individuals and lowering sodium in the diet will reduce blood pressure in some hypertensive persons.
Whether the recommendation to lower sodium intake applies to athletes is another matter. Endurance exercise is associated with significant sodium loss through sweating, which needs to be replaced in the diet (Sawka et al., 2007). Recommendations for dietary sodium content for athletes need to take exercise-related sodium losses into account as well as the generally low hypertension risk in athletes (Franklin et al., 2004).
This sports science exchange article will focus on the on physiological mechanisms controlling thirst and body fluid regulation and how these mechanisms function during exercise. Sodium regulation in active individuals and how dietary sodium supports thirst and fluid balance during competition and training will also be addressed.
MECHANISMS CONTROLLING THIRST AND BODY FLUID REGULATION
One of the key functions of sodium (Na+) is to regulate the body’s osmotic balance (related to the concentration of ions and solutes in the body fluid compartments and their movement between compartments). Centers in the brain detect changes in blood tonicity (related to the amount of sodium in the blood). These centers use neural mechanisms to trigger central brain responses involved in the regulation of body water, electrolytes and blood pressure, including thirst stimulation and angiotensin II release (which reduces water and sodium loss). The changes in blood sodium are perceived as an osmotic stimulus, which is sensed by central osmo-Na+ receptors, nerves that are responsible for detecting the concentration of the interstitial fluid. Experiments in the 1940s were the first to describe osmotic mechanisms, or "osmoreceptors" (Verney, 1947), while later studies implicated these centers in the regulation of thirst and drinking (Figure 1). Nerves that detect changes in stretch that occur with changes in central blood volume, called volume-pressure receptors are located in the heart ("baroreceptors"). The acute changes in central volume or blood sodium concentration initiate a global response including adjustments in thirst and sodium appetite, sympathetic nervous system activity, renal fluid regulating hormones and the renin-angiotensin-aldosterone system (McKinley et al., 2004).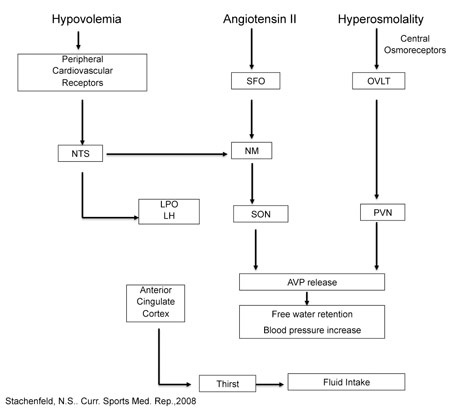 Figure 1. Schematic of central regulation of body fluid regulation in response to acute changes in sodium and volume. Text and Figure reprinted with permission from Stachenfeld. Copyright (2008) (Stachenfeld, 2008) American College of Sports Medicine, U.S.A. Figure 1 based on original figure by Gary W. Mack (with permission).
The OVLT (organum vasculosum of the lamina terminalis) is a circumventricular organ located outside the blood-brain barrier (BBB), in the anteroventral part of the third ventricle that is an essential component of the osmotic thirst sensation pathway. Osmotic information from the OVLT is transmitted neurally to the hypothalamus and ultimately results in thirst, drinking and arginine vasopressin (AVP) release. The median preoptic nucleus (NM) is responsible for initiating drinking in response to volumetric and angiotensinergic thirst stimulation. Through these mechanisms, the NM is utilized by both the subfornical organ (SFO) and the nucleus of the solitary tract (NTS), structures at the center of sodium appetite and thirst regulation. Changes in volume are initiated by the kidneys, and stimulated by angiotensin outside the BBB. The SFO sends a message across the BBB to the NM, which then initiates volumetrically controlled thirst and drinking responses. Atrial baroreceptors also send a signal to the NTS. In addition to stimulating thirst, angiotensin stimulates the SFO and causes fluid regulating hormones to be secreted by the pituitary and adrenal glands, increases blood pressure and eventually causes the kidney to stop secreting sodium and water, which, in turn, decreases both salt appetite and water intake. The paraventricular (PVN) and supraoptic nuclei (SON), both located in the hypothalamus, signal the release of AVP by the posterior pituitary. Thus both the PVN and SON also represent important structures involved in the control of water and sodium regulation because AVP has powerful effects on both blood pressure and free water retention. Finally, the anterior cingulate cortex is involved in the relay of neural signals between the right and left hemispheres of the brain. This part of the brain is important for decision-making, and plays an important role in sensing thirst and initiating drinking.
Figure 1. Schematic of central regulation of body fluid regulation in response to acute changes in sodium and volume. Text and Figure reprinted with permission from Stachenfeld. Copyright (2008) (Stachenfeld, 2008) American College of Sports Medicine, U.S.A. Figure 1 based on original figure by Gary W. Mack (with permission).
The OVLT (organum vasculosum of the lamina terminalis) is a circumventricular organ located outside the blood-brain barrier (BBB), in the anteroventral part of the third ventricle that is an essential component of the osmotic thirst sensation pathway. Osmotic information from the OVLT is transmitted neurally to the hypothalamus and ultimately results in thirst, drinking and arginine vasopressin (AVP) release. The median preoptic nucleus (NM) is responsible for initiating drinking in response to volumetric and angiotensinergic thirst stimulation. Through these mechanisms, the NM is utilized by both the subfornical organ (SFO) and the nucleus of the solitary tract (NTS), structures at the center of sodium appetite and thirst regulation. Changes in volume are initiated by the kidneys, and stimulated by angiotensin outside the BBB. The SFO sends a message across the BBB to the NM, which then initiates volumetrically controlled thirst and drinking responses. Atrial baroreceptors also send a signal to the NTS. In addition to stimulating thirst, angiotensin stimulates the SFO and causes fluid regulating hormones to be secreted by the pituitary and adrenal glands, increases blood pressure and eventually causes the kidney to stop secreting sodium and water, which, in turn, decreases both salt appetite and water intake. The paraventricular (PVN) and supraoptic nuclei (SON), both located in the hypothalamus, signal the release of AVP by the posterior pituitary. Thus both the PVN and SON also represent important structures involved in the control of water and sodium regulation because AVP has powerful effects on both blood pressure and free water retention. Finally, the anterior cingulate cortex is involved in the relay of neural signals between the right and left hemispheres of the brain. This part of the brain is important for decision-making, and plays an important role in sensing thirst and initiating drinking.
SODIUM LOSS DURING EXERCISE
Sodium loss occurs in both elite and recreational athletes during endurance exercise. This paper deals with endurance exercise, but most of the content also relates to stop-and-go sports that involve high intensity intermittent exercise that lasts 2-3 h. This loss is exaggerated during exercise in hot environments and is affected by training status and heat acclimatization. Moreover, during exercise, most extracellular fluid volume loss is a direct function of the sweat sodium loss (Nose et al., 1988b). The amount of sodium that is lost depends on the sweating rate and the concentration of sodium in the sweat. Because sweating is related to genetic factors, diet, body weight, heat acclimatization and other physiological traits, there is a wide variation in the amount of sweating and sodium loss across individuals. This variability across individuals persists even when the intensity and type of activity are the same and are performed in the same environmental conditions. However, some sodium will be lost during endurance exercise in all athletes and the extent of the loss determines how much sodium needs to be replaced (Sawka et al., 2007). While some of the sodium released in sweat is reabsorbed by the sweat gland, sweat sodium loss during exercise (especially in the heat) occurs more rapidly than it can be reabsorbed, so much of the sodium in sweat is lost. Heat acclimatization improves sodium and chloride reabsorption so heat acclimatized individuals usually have a more dilute sweat for a given sweating rate (Buono et al., 2007).
SODIUM INGESTION IN ATHLETES
Participation in an endurance event lasting 2 h can result in the loss of ~70 mEq or 1.6 g of sodium, concomitant with a body water loss of ~ 2-3% body mass, and an increase in plasma sodium concentration of on average 5-7 mEq/L. The American College of Sports Medicine position stand “Exercise and Fluid Replacement” (Sawka et al., 2007) provides specific information on the sweat sodium lost during various activities. Although there is wide variation across individuals and activities, the ”position stand” indicates that athletes can lose as much as 5 g sodium in sweat during a single high intensity workout. Thus, during endurance exercise, sodium ingestion plays an important role to minimize dehydration and assist with body fluid maintenance and electrolyte balance. Sodium ingestion not only replaces some of the sodium lost in sweat, but supports an osmotic thirst and dipsogenic or thirst inducing drive to motivate athletes to continue drinking and increase fluid consumption over that of water alone (Baker et al., 2005).
THIRST
Thirst sensation is highly sensitive to changes in sodium within the vascular system, with only a 2-3% change in plasma tonicity required to induce thirst in humans (Figure 2). There are also “volumetric” thirst mechanisms that sense changes in central volume related to plasma volume losses, but volume, or baroreceptor mediated changes require a much greater stimulus to affect thirst relative to the osmotic mechanisms. Fluid restoration is assisted by thirst mechanisms during endurance exercise lasting under 90-120 min, but to optimize performance athletes should plan a drinking program along with sodium replacement in the diet. For exercise in the heat, or for long-term events during which large amounts of water and sodium are lost through sweat, the athlete must make a conscious effort to replenish both water and sodium because a number of factors can interfere with thirst sensation. For example, the act of drinking (swallowing) causes immediate thirst suppression through an overriding oropharyngeal reflex before a significant change in blood tonicity occurs. In addition, early thirst suppression also occurs during recovery from dehydrating exercise, when fluid movement across vascular compartments causes rapid plasma sodium concentration and plasma volume restoration, even in the face of continued extra- and intracellular dehydration (Baker et al., 2005). Both during (Baker et al., 2005) and following (Nose et al., 1988b) dehydrating exercise, sodium ingestion is a successful method to avoid this “involuntary dehydration” and replenish plasma volume and osmolality more completely or avoid significant sodium losses. A series of experiments demonstrated that adding sodium to water during recovery from dehydrating exercise improves overall hydration by maintaining thirst stimulation and enlisting sodium regulating hormones to improve renal sodium water and sodium retention (Nose et al., 1988a, b, c).
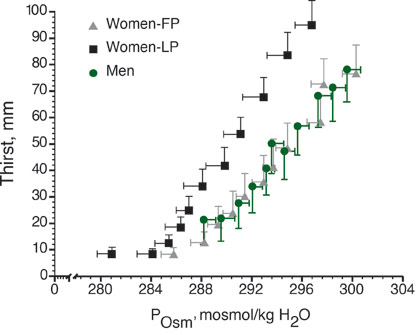
Figure 2. Thirst as a function of plasma osmolality (POsm, mosmol/kg H2O) in men and in women in the follicular (FP) and luteal (LP) of the menstrual cycle. Thirst is measured on a sensory scale in millimeters.
EXERCISE ASSOCIATED HYPONATREMIA (EAH)
As described earlier, finishing a marathon or other endurance event typically results in ~ 2-3% loss in total body water concomitant with increases in plasma sodium concentration on average ~ 5-7 mEq/L. Some athletes (1-13%) reduce sodium concentration by ≥ 5 mEq/L relative to pre-race values at the end of endurance exercise (Almond et al., 2005; Speedy et al., 2001), usually the result of excess hypotonic fluid ingestion accompanied by significant water retention. This condition, exercise associated hyponatremia (EAH) can induce severe consequences (cerebral edema and metabolic encephalopathy, permanent brain damage) from which some athletes do not recover. Thus, although EAH is less common than dehydration, its consequences can be more severe. EAH is also associated with several serious symptoms, such as malaise, nausea, light-headedness, dizziness and fatigue. Data from field studies have suggested EAH may be a variant of the Syndrome of Inappropriate Antidiuretic Hormone (SIADH), described as persistently high levels of the hormone ADH (or vasopressin, AVP) despite low levels plasma osmolality and sodium and significant body water retention. However, a recent prospective study demonstrated that although water retention, and not sodium loss, was the primary contributor to the lower exercise sodium concentration in women at risk for EAH, AVP responses were similar in women with high and low EAH risk (Stachenfeld & Taylor, 2009). The best way to reduce EAH risk is to be sure that fluid intake does not greatly exceed fluid loss. Athletes can track this by monitoring fluid intake as well as the volume and concentration (color) of urine. Mechanisms contributing to EAH are difficult to study because most investigations in the area are retrospective: that is, athletes who have become hyponatremic during a long distance event are recruited at the finish line, or reported upon while receiving treatment in medical tents. These studies have their limitations in that they may miss subjects with EAH who are asymptomatic and recover on their own and therefore, these studies may be biased by studying only extreme EAH or athletes who are more sensitive to EAH and experience symptoms with only small changes in plasma sodium.
BLOOD PRESSURE
In approximately one third of the population, regular ingestion of sodium is associated with hypertension (“sodium sensitive hypertension”) (Sacks et al., 2001). The kidney is of primary importance in sodium sensitive hypertension due to its ability to regulate sodium. The epithelial sodium channel in the renal collecting duct is a primary mechanism of sodium control, and malfunction in this channel leads to hypertension. The epithelial sodium channel is under the direct control of the primary sodium regulating hormone aldosterone. More recent studies have indicated that central control of the sympathetic nervous system also plays an important role in the genesis of salt sensitive hypertension. Rapid sodium infusions are used in humans and animals because these sodium infusions cause acute increases in plasma sodium and stimulate the blood pressure regulatory system. Studies in animals have demonstrated that blood pressure increases are mediated by central osmoreceptor input to sympathetic nerves (Brooks et al., 2001). In humans, a large acute sodium load transiently increased blood pressure in men (this is not a consistent finding in women), muscle sympathetic nerve activity (MSNA) (Farquhar et al., 2006) and baroreflex control of sympathetic outflow (Charkoudian et al., 2005). Interestingly, sympathetic outflow in response to a sodium load is moderated by the extent of plasma volume contraction (Charkoudian et al., 2003) or expansion (Charkoudian et al., 2005; Farquhar et al., 2006), supporting a role for baroreceptors in the blood pressure responses in such instances as dehydration (Charkoudian et al., 2003).
In healthy people, acute sodium ingestion does not cause sustained hypertension. Athletes and most normal weight, active people have a lower hypertension risk because studies have consistently shown that blood pressure can be lowered by weight loss and regular aerobic exercise (Franklin et al., 2004). Moreover, sodium is an essential component of most athletes’ diets because sodium ingestion helps restore total body water and fluid-electrolyte balance by replacing sweat sodium losses. It is important, however, to note that athletes are not immune to hypertension, and athletes who participate in sports in which large muscle mass and weight lifting are required should monitor blood pressure closely. Sodium intake in this subset of athletes should be considered with the same risks as an inactive person, and be proportional to sweat losses.
PRACTICAL APPLICATIONS
- There is large individual variability across athletes and/or active people in sodium losses through sweating, so athletes should evaluate sodium and fluid losses during workouts.
- Athletes should practice their fluid replenishment regimen as they are training for the event, and learn which methods of sodium provision (drinks, snacks, etc.) will be provided by the race organizers along the route.
- Combining urine examination to determine how dark or light the urine is with measurement of a first morning body weight can provide an indication of any significant changes in hydration status. Also, using changes in body weight together with urine color as biomarkers provides significantly more insight than using them individually.
- Sodium ingestion during long term exercise can:
- One liter (34 oz) of a sports drink containing 20 mEq/L of sodium will typically provide 460 mg of sodium.
- Although body fluid status related to dehydration and EAH (often a result of excessive drinking) is completely different, some of the symptoms, such as malaise, nausea, light-headedness, dizziness and fatigue can overlap. Therefore, if changes in body weight or a blood sample cannot be attained, assessment of fluid intake and urination during the exercise bout is important before deciding on treatment.
- Athletes who lose large volumes of sweat should consider ingesting additional sodium in the form of sports drinks with greater sodium content or bars, gels, electrolyte powders, salty snacks or tablets that provide extra sodium.
- Many sports drinks are hypotonic to plasma, so athletes who use sports drinks should not assume that they are immune to EAH.
SUMMARY
Thirst, drinking and hormonal regulation of fluid balance are tightly controlled through central mechanisms (Figure 1). Plasma sodium concentration is a potent thirst stimulus at rest, during exercise and in the post-exercise rehydration period. Sodium ingestion is an excellent means to continue the dipsogenic or thirst inducing drive to ensure adequate rehydration. The sodium can come as a part of the athlete’s diet, but after long lasting endurance exercise, especially in the heat, the athlete may want to consider salty snacks or drinks with electrolytes. Sodium ingestion and maintenance of sodium concentration also stimulates renal mechanisms to reduce water loss in urine and conserve fluid.
REFERENCES
Almond, C.S.D., A.Y. Shin, E.B. Fortescue, R.C. Mannix, D.Wypij, B.A. Binstadt, C.N. Duncan, D.P. Olson,, A.E. Salerno, J.W. Newburger, and D.S. Greenes (2005). Hyponatremia among runners in the Boston Marathon. N. Engl. J. Med. 352:1550-1556.
Baker, L.B., T.A.Munce, and W.L. Kenney (2005). Sex differences in voluntary fluid intake by older adults during exercise. Med. Sci. Sports Exerc. 37:789-796.
Brooks, V.L., K. Scrognin, and D.F. McKeigh (2001). The interaction of angiotensin II and osmolality in the generation of sympathetic tone during changes in dietary salt intake. An hypothesis. Ann. New York Acad. Sci. 940:380-394.
Buono, M.J., K.D. Ball. and F.W. Kolkhorst (2007). Sodium ion concentration vs. sweat rate relationship in humans. J. Appl. Physiol. 103:990-994.
Charkoudian, N., J.R.Halliwill, B.J. Morgan, J.H. Eisenach, and M.J. Joyner (2003). Influences of hydration on post-exercise cardiovascular control in humans. J. Physiol. 552:635-644.
Charkoudian, N., J.H. Eisenach, M.J. Joyner, S.K. Roberts, and D.E. Wick (2005). Interactions of plasma osmolality with arterial and central venous pressures in control of sympathetic activity and heart rate in humans. Am. J. Physiol. 289:H2456-2460.
Farquhar, W.B., M.M. Wenner, E.P. Delaney, A.V. Prettyman, and M.E. Stillabower (2006). Sympathetic neural responses to increased osmolality in humans. Am. J. Physiol. 291:H2181-2186.
Franklin, B.A., R. Fagard, W.B. Farquhar, G.A. Kelley, and C.A. Ray (2004). American College os Sports Medicine position stand. Exercise and hypertension. Med. Sci.Sports Exerc. 36:533-553.
McKinley, M.J., M.J. Cairns, D.A. Denton, G. Egan, M.L. Mathai, A.Uschakov, J.D.Wade, R.S. Weisinger, and B.J. Oldfield (2004). Physiological and pathophysiological influences on thirst. Physiol. Behav. 81:795-803.
Nose, H., G.W.Mack, X.Shi, and E.R. Nadel (1988a). Shift in body fluid compartments after dehydration in humans. J. Appl. Physiol. 65:318-324.
Nose, H., G.W.Mack, X, Shi, and E.R. Nadel (1988b). Role of osmolality and plasma volume during rehydration in humans. J. Appl. Physiol. 65:325-331.
Nose, H., G.W. Mack, X. Shi X, and E.R. Nadel (1988c). Involvement of sodium retention hormones during rehydration and deydration in humans. J. Appl. Physiol. 65:332-336.
Sacks, F.M., L.P. Svetkey, W.M. Vollmer, L.J. Appel, G.A. Bray, D. Harsha, E. Obarzanek, P.R. Conlin, E.R. Miller, D.G. Simons-Morton, N. Karanja, P.-H. Lin, M. Aickin, M.M. Most-Windhauser, T.J. Moore, M.A. Proschan, and J.A. Cutler (2001). Effects on blood pressure of reduced dietary sodium and the dietary approaches to stop hypertension (DASH) diet. New Engl. J. Med. 344:3-10.
Sawka, M.N., L.M. Burke, E.R. Eichner, R.J. Maughan, S.J. Montain, and N.S. Stachenfeld (2007). American College of Sports Medicine position stand. Exercise and fluid replacement. Med. Sci. Sports Exerc. 39:377-390.
Speedy, D.B., T.D. Noakes, and C. Schneider (2001). Exercise-associated hyponatremia: A review. Emerg. Med. 13:17-27.
Stachenfeld, N.S. (2008). Acute effects of sodium ingestion on thirst and cardiovascular function. Curr. Sports Med. Rep. 7:S7-13.
Stachenfeld, N.S., and H.S. Taylor (2009). Sex hormone effects on body fluid and sodium regulation in women with and without exercise-associated hyponatremia. J. Appl. Physiol. 107:864-872.
Verney, E. (1947). The antidiuretic hormone and the factors which determine its release. Proc. Soc. Lond. B Biol. 135:25-105.








